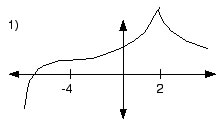
BC Calculus: Graphing f From Information About f' and f''

  1. Given the following table of values, graph a continuous function \(f\).
    \(x < -4\) \(x = -4\) \(-4 < x < 2\) \(x = 2\) \(x \gt 2\)
    \(f'\)
    +
    1
    +
    DNE
    -
    \(f''\)
    -
    0
    +
    DNE
    +
    2. Solution
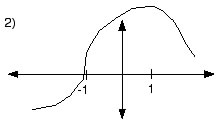
  2. Given the following table of values, graph a continuous function \(f\).
    \(x < -1 \) \(x = -1\) \(-1 < x < 1 \) \(x = 1 \) \(x \gt 1 \)
    \(f'\)
    +
    DNE
    +
    0
    -
    \(f''\)
    +
    DNE
    -
    -2
    -
    3. Solution
  3. Given the following table of values, indicate where \(f\) has relative extrema.
    \(x = 2\) \(2 < x < 5\) \(x = 5\) \(5 < x < 8\) \(x = 8 \)
    \(f'\)
    +
    +
    0
    -
    -
    4. Solution \(f\) has relative mins at \(x = 2\) and \(x = 8\) and a relative max at \(x = 5\).