BC Calculus: AP Review Problems for Chapter 6

    Questions come from Advanced Placement Calculus Tests as Indicated.

    Answer each of the following three questions on separate sheets of paper, one question per page. Be prepared to detach the pages from your notebooks. You'll be correcting each other's problems.

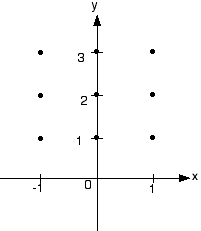
  1. 1998 BC 4 (Calculator Active) Consider the differential equation given by \( \frac{dy}{dx} = \frac{xy}{2}\).
    1. On the axes provided below, sketch a slope field for the given differential equation at the nine points indicated.
    2. Let \(y = f(x)\) be the particular solution to the given differential equation with the initial condition \(f(0) = 3\). Use Euler's method starting at \(x = 0\) with a step size of 0.1 to approximate \(f(0.2)\). Show the work that leads to your answer.
    3. Find the particular solution \(y = f(x)\) to the given differential equation with the initial condition \(f(0) = 3\). Use your solution to find \(f(0.2)\).
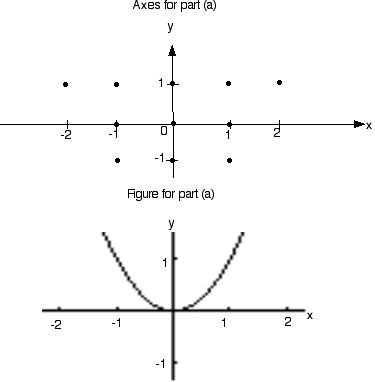
  2. 2000 BC 6 (Calculator Inactive) Consider the differential equation given by \( \frac{dy}{dx} = x(y - 1)^2\)
    1. On the axes below, sketch a slope field for the given differential equation at the eleven points indicated.
    2. Use the slope field for the given differential equation to explain why a solution could not have the graph shown below.
    3. Find the particular solution \(y = f(x)\) to the given differential equation with the initial condition \(f(0) = -1\).
    4. Find the range of the solution found in part (c).
  3. 2002 BC 5 (Form B) (Calculator Inactive) Consider the differential equation \(\frac{dy}{dx} = \frac{3 - x}{y}\).
    1. Let \(y = f(x)\) be the particular solution to the given differential equation for \(1 < x < 5\) such that the line \(y = -2\) is tangent to the graph of \(f\). Find the x-coordinate of the point of tangency, and determine whether \(f\) has a local maximum, local minimum, or neither at this point. Justify your answer.
    2. Let \(y = g(x)\) be the particular solution to the given differential equation for \(-2 < x < 8\) with the initial condition \(g(6) = -4\). Find \(y = g(x)\).