BC Calculus More Area-Volume Problems

• Class: 5H: BC Calculus
• Author: Peter Atlas
• Text: Calculus Finney, Demana, Waits, Kennedy

CALCULATOR INACTIVE

1. (1980 AB1) Let \( R \) be the region enclosed by the graphs of \( \displaystyle y = x^3\) and \( \displaystyle y = \sqrt{x}\).
   
   1. Find the area of the region \( R \) .
   Solution
   \( \displaystyle x^3 = \sqrt{x} \implies x = {0, 1}. \int_{0}^{1} (x^{\frac{1}{2}} - x^3) \, dx = \left. \frac{2}{3}x^{\frac{3}{2}} - \frac{x^4}{4} \right|_0^1 = \frac{2}{3}1^{\frac{3}{2}} - \frac{1^4}{4} \)
   2. Find the volume of the solid generated by revolving \( R \) about the x-axis.
   Solution
   \( \displaystyle \pi \int_{0}^{1} \left( (\sqrt{x})^2 - (x^3)^2 \right) \, dx = \pi \int_{0}^{1} (x - x^6) \, dx =\left. \pi \left( \frac{x^2}{2} - \frac{x^7}{7} \right) \right|_0^1 = \pi \left( \frac{1^2}{2} - \frac{1^7}{7} \right) \)
2. (1981 AB2) Let \( R \) be the region in the first quadrant enclosed by the graphs of \( \displaystyle y = 4 - x^2\) and, \( \displaystyle y = 3x\), and the y-axis.
   
   1. Find the area of \( R \) .
   Solution
   \( \displaystyle 4 - x^2 = 3x \implies x = 1. \int_{0}^{1} (4 - x^2 - 3x) \, dx \) = \( \displaystyle \left. 4x - \frac{ x^3}{3} - \frac{3x^2}{2} \right|_0^1 \) = \( \displaystyle 4\cdot 1 - \frac{ 1^3}{3} - \frac{3 \cdot 1^2}{2} \)
   2. Find the volume of the solid formed by revolving the region \( R \) about the x-axis.
   Solution
   \( \displaystyle \pi \int_{0}^{1} \left( (4 - x^2)^2 - (3x)^2 \right) \, dx \) = \( \displaystyle \pi \int_{0}^{1} \left( 16 - 8x^2 + x^4 - 9x^2 \right) \, dx \) = \( \displaystyle \pi \left. \left( 16x - \frac{8}{3}x^3 + \frac{1}{5}x^5 - 3x^3 \right) \right|_0^1 \) = \( \displaystyle \pi \left( 16 - \frac{8}{3}1^3 + \frac{1}{5}1^5 - 3 \cdot 1^3 \right) \)
3. (1981 BC6)
   
   1. A solid is constructed so that it has a circular base of radius \( r \) centimeters and every plane section perpendicular to a certain diameter of the base is a square, with a side of the square being a chord of the circle. Find the volume of the solid.
   Solution
   \( \displaystyle 2 \int_0^r \left( 2 \sqrt{r^2 - x^2} \right) ^2 \, dx \) = \( \displaystyle 2 \int_0^r 4 \left( r^2 - x^2 \right) \, dx \) = \( \displaystyle 8 \left. \left( r^2x - \frac{x^3}{3} \right) \right|_0^r \) = \( \displaystyle 8 \left( r^3 - \frac{r^3}{3} \right) \)
   2. If the solid described in part (a) expands so that the radius of the base increases at a constant rate of \( \frac{1}{2}\) centimeters per minute, how fast is the volume changing when the radius is 4 centimeters?
   Solution
   Given \( \displaystyle \frac{dr}{dt} = \frac{1}{2}\), find \( \displaystyle \frac{dV}{dt}\) when \( \displaystyle r = 4\). From part (a) we have that \( \displaystyle V = \frac{16r^3}{3} \implies \frac{dV}{dt} = \frac{16}{3} \left( 3r^2 \right) \frac{dr}{dt}\). At \( \displaystyle r = 4, \frac{dV}{dt} = \frac{16}{3} \left( 3 \cdot 4^2 \right) \frac{1}{2} \frac{\text{cm}^3}{\text{min}}\)
4. (1982 AB3/BC1) Let \( R \) be the region in the first quadrant enclosed by the graph of \( \displaystyle y = \tan {x}\), the x-axis, and the line \( \displaystyle x = \frac{\pi}{3}\).
   
   1. Find the area of \( R \) .
   Solution
   \( \displaystyle \left. \int_0^{\frac{\pi}{3}} \tan{x} \, dx = \displaystyle \ln { \left| \sec{x} \right| } \right|_0^{\frac{\pi}{3}} \) = \( \ln { | \sec{\frac{\pi}{3} } | } - \ln { | \sec{0} | }\)
   2. Find the volume of the solid formed by revolving \( R \) about the x-axis.
   Solution
   \( \displaystyle \pi \int_0^{\frac{\pi}{3}} \tan^2 {x} \, dx \) = \( \displaystyle \pi \left. \int_0^{\frac{\pi}{3}} \left( \sec^2 {x} - 1 \right) \, dx = \displaystyle \pi \left( \tan {x} - x \right) \right|_0^{\frac{\pi}{3}} \) = \( \displaystyle \pi \left( \tan {\frac{\pi}{3}} - \frac{\pi}{3} \right) \)
5. (1983 AB4) Let \( R \) be the region between the graph of \( \displaystyle x^{\frac{1}{2}} + y ^{\frac{1}{2}} = 2\) and the x-axis from \( \displaystyle x = 0\) to \( \displaystyle x = 1\).
   
   1. Find the area of \( R \) by setting up and integrating a definite integral.
   Solution
   \( \displaystyle \int_0^1 \left( 2 - x^{\frac{1}{2}} \right) ^2 \, dx \) = \( \displaystyle \int_0^1 \left( 4 - 4 x^{\frac{1}{2}} + x \right) \, dx \) = \( \displaystyle \left. 4x - \frac{8}{3} x^{\frac{3}{2}} + \frac{1}{2}x^{2} \right|_0^1 \) = \( \displaystyle 4 \cdot 1 - \frac{8}{3} 1^{\frac{3}{2}} + \frac{1}{2}1^{2} \)
   2. Set up, but do not integrate, an integral expression in terms of a single variable for the volume of the solid formed by revolving the region \( R \) about the x-axis.
   Solution
   \( \displaystyle \pi \int_0^1 \left( 4 - 4x^\frac{1}{2} + x \right) ^2 \, dx \)
   3. Set up, but do not integrate, an integral expression in terms of a single variable for the volume of the solid formed by revolving the region \( R \) about the line \( \displaystyle x = 1\).
   Solution
   \( \displaystyle 2 \pi \int_0^1 \left(1 - x \right) \left( 2 - x^{\frac{1}{2}} \right) ^2 \, dx \)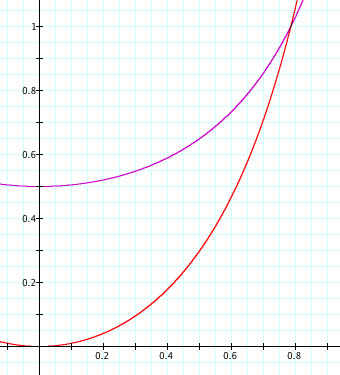
6. (1986 AB6/BC3) Let \( R \) be the region in the first quadrant enclosed by the graphs of \( \displaystyle y = \tan^2 {x}, y = \frac{1}{2} \sec ^2 {x}\), and the y-axis, as in the figure below.

   

   1. Find the area of region \( R \) .
   Solution
   \( \displaystyle \tan^2 {x} = \frac{1}{2} \sec^2 {x} \implies x = \frac{\pi}{4}.\) So \( \displaystyle \int_0^{\frac{\pi}{4}} \left( \frac{1}{2}\sec^2{x} - \tan^2{x} \right) \, dx \) = \( \displaystyle \int_0^{\frac{\pi}{4}} \left( \frac{1}{2}\sec^2{x} - (\sec^2{x} - 1) \right) \, dx \) = \( \displaystyle \int_0^{\frac{\pi}{4}} \left( -\frac{1}{2}\sec^2{x} + 1 \right) \, dx \) = \( \displaystyle \left. \left( -\frac{1}{2}\tan{x} - x \right) \right|_0^{\frac{\pi}{4}} \) = \( \displaystyle -\frac{1}{2}\tan{\frac{\pi}{4}} - \frac{\pi}{4} \)
   2. Set up, but do not integrate, an integral expression in terms of a single variable for the volume of the solid formed by revolving the region \( R \) about the x-axis.
   Solution
   \( \displaystyle \pi \int_0^{\frac{\pi}{4}} \left( \frac{1}{2}\sec^2{x} \right) ^2 - \left( \tan^2{x} \right) ^2 \, dx \) =