BC Calculus: Midyear Review Worksheet 2

Questions have been taken from Lifshitz, Maxine, Calculus AB/BC Preparing for the Advanced Placement Examinations; Amsco, 2004

The following should be done without a calculator .

  1. If \( \displaystyle xy - y = 2x + 4, \frac{dy}{dx} = \)
    1. \( \displaystyle \frac{y - 2}{x - 1}\)
    2. \( \displaystyle \frac{2 - y}{x - 1}\)
    3. \( \displaystyle \frac{y - 6}{x - 1}\)
    4. \( \displaystyle \frac{2}{x - 1}\)
    5. \( \displaystyle \frac{y - 2}{x + 1}\)
    2. Solution B
  2. Let \(f(x)\) be an odd function and \(g(x)\) be even. Which of the following statements are true?
    1. \( \displaystyle \int_{-2}^{2} f(x) \, dx = 0\)
    2. \( \displaystyle \int_{-2}^{2} g(x) \, dx = 0\)
    3. \( \displaystyle \int_{-2}^{2} f(x)g(x) \, = 0\)
    1. II
    2. III
    3. I and II
    4. I and III
    5. I, II, and III
    3. Solution D
  3. \( \displaystyle \lim_{x \to 0} \frac{\sin{3x}}{5x} =\)
    1. \( \displaystyle \frac{3}{5} \)
    2. \( \displaystyle \frac{5}{3}\)
    3. 3
    4. 5
    5. no limit exists
    4. Solution A
  4. For which of the following x-values on the graph of \(y = 2x - x^2\) is \( \displaystyle \frac{dy}{dx}\) the largest?
    1. -2.7
    2. -2.2
    3. 0
    4. 1
    5. 2.7
    5. Solution A
  5. If \( \displaystyle y = e^{2x} + \tan {(2x)}\), then \(y'( \pi ) =\)
    1. \( \displaystyle 2e^{2\pi}\)
    2. \( \displaystyle e^{2\pi} + 1\)
    3. \( \displaystyle 2e^{2\pi} + 2\)
    4. \( \displaystyle 2e^{\pi} - 2\)
    5. 0
    6. Solution C
  6. Write the equation of the line tangent to \(y = e^{x+1}\) at \(x = 0\).
    1. \( y = ex + e\)
    2. \( y = x\)
    3. \( y = x + 1\)
    4. \( y = x + e\)
    5. \( y = ex + 1\)
    7. Solution A
  7. If the acceleration of a particle is given by \( a(t) = 2e^t \) and at \(t = 1\) the velocity is 2, then \(v(0)\) is
    1. 0
    2. \( 2 - 2e\)
    3. \( \displaystyle 2 - \frac{e}{2}\)
    4. \( 4 - 2e\)
    5. 2
    8. Solution D
  8. If \( 3xy + 2y^2 = 5\), find \( \displaystyle \frac{dy}{dx}\) at (1, 1)
    1. \( \displaystyle -\frac{3}{7}\)
    2. 0
    3. \( \displaystyle \frac{3}{7}\)
    4. 7
    5. undefined
    9. Solution A
  9. The graph of \( \displaystyle y = \ln{\frac{1 - x}{x + 1}}\) has vertical asymptote(s) at
    1. \( x = 1\)
    2. \( x = 0\)
    3. \( x = \pm 1\)
    4. \( x = -1\)
    5. no vertical asymptotes
    10. Solution C
  10. \( \displaystyle \frac{d}{dt} \int_{t}^{t^2} \frac{1}{x} \, dx = \)
    1. \( \displaystyle \frac{1}{t^2}\)
    2. \( \ln {t}\)
    3. \( \ln{(t^2)}\)
    4. \( \displaystyle \frac{1}{t}\)
    5. \( \displaystyle \ln{\left(\frac{1}{t}\right)}\)
    11. Solution D
  11. \( \displaystyle \lim_{h \to 0} \frac{\cos{ \left( \frac{\pi}{4} + h \right) } - \cos {\left( \frac{\pi}{4} \right)}}{h}\)
    1. \( \displaystyle -\frac{\sqrt{3}}{2}\)
    2. \( \displaystyle -\frac{\sqrt{2}}{2}\)
    3. 0
    4. \( \displaystyle \frac{\sqrt{2}}{2}\)
    5. 1
    12. Solution B
  12. \( \displaystyle \int (3x^2 - \cos{x }) \, dx = \)
    1. \( 6x +\sin{x} + C\)
    2. \( x^3+\sin{ x} + C\)
    3. \( x^3-\sin{ x} + C\)
    4. \( 6x -\sin{ x} + C\)
    5. \( 3x^3-\sin{ x} + C\)
    13. Solution C
  13. Find the area under the curve \( y = x^2+ 1\) on the interval [1, 2].
    1. \( \displaystyle \frac{7}{3}\)
    2. 3
    3. \( \displaystyle \frac{10}{3} \)
    4. 4
    5. 7
    14. Solution C
  14. \( \displaystyle \int_{-1}^{2} \frac{x}{x^2+ 1} \, dx = \)
    1. \( \displaystyle \ln {\frac{2}{5}} \)
    2. 0
    3. \( \displaystyle \frac{1}{2} \ln {\frac{5}{2}} \)
    4. \( \displaystyle \frac{1}{2} \ln {3} \)
    5. undefined
    15. Solution C
  15. \( \displaystyle \int_{0}^{1} e^{3x + 2} \, dx = \)
    1. \( \displaystyle \frac{1}{3} e^5 \)
    2. \( \displaystyle \frac{1}{3}(e^5 - e^2)\)
    3. \( \displaystyle \frac{1}{3}(e^5 - 1 )\)
    4. \( e^5 - 1\)
    5. \( e^5 - e^2\)
    16. Solution B
  16. If \( \displaystyle y =\sin^2{(5x)}, \frac{dy}{dx} = \)
    1. \( 5\sin{ (10x)}\)
    2. \( 5\cos {(5x)}\)
    3. \( 5\sin{(5x)}\)
    4. \( 10\sin{(10x)}\)
    5. \( 10\sin^2{(5x)}\)
    17. Solution A
  17. For what values of \(x\) is \(f(x) = 2x^3- x^2 + 2x\) concave up?
    1. \( \displaystyle x < \frac{1}{6}\)
    2. \( x < 0\)
    3. \( x > 0\)
    4. \( \displaystyle x > \frac{1}{6}\)
    5. \( x > 6\)
    18. Solution D
  18. This problem refers to the graph of the velocity, \(v(t)\) of an object at time \(t\). The graph consists of two segments: one joining (0, 20) to (5, 20), and a second joining (5, 20) to (10, -20). If \(x(t)\) is the position of the object at time \(t\), and \(a(t)\) is the acceleration of the object at time \(t\), which of the following is true?
    1. \( v(5) > v(2)\)
    2. \( x(5) > x(2)\)
    3. \( a(6) > a(2)\)
    4. \( x(10) < x(5)\)
    5. \( a(9) > a(6)\)
    19. Solution B
  19. Referring to the velocity as described in problem 18, \( \int_{0}^{10} v(t) \, dt = \)
    1. 0
    2. 5
    3. 50
    4. 75
    5. 100
    20. Solution E
  20. If \(f(1) = 2\) and \(f'(1) = 5\), use the equation of the line tangent to the graph of \(f\) at \(x = 1\) to approximate \(f(1.2)\)
    1. 1
    2. 1.2
    3. 3
    4. 5.4
    5. 9
    21. Solution C
  21. The equation of the line tangent to \(y = \tan^2{(3x)}\) at \( \displaystyle x = \frac{\pi}{4}\) is
    1. \( y = -12x + 3 \pi - 1\)
    2. \( y = -12x + 3 \pi + 1\)
    3. \( \displaystyle y = -6x + \frac{3\pi}{2} + 1\)
    4. \( y = -12x + 3 \pi + 3\)
    5. \( y = -12x + \pi + 3\)
    22. Solution B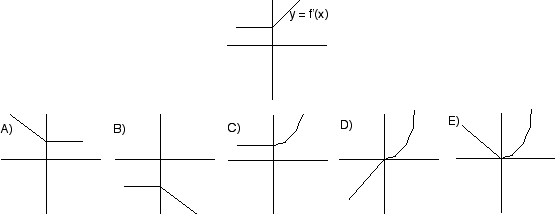
  22. The graph of \(f'(x)\) is shown below. Which of the following choices could be the graph of \(f\)?
    23. Solution D
  23. At what value of \(x\) is the line tangent to the graph of \(y = x^2 + 3x + 5\) perpendicular to the line \(x - 2y = 5\)?
    1. \( \displaystyle -\frac{5}{2}\)
    2. -2
    3. \( \displaystyle -\frac{1}{2}\)
    4. \( \displaystyle \frac{1}{2}\)
    5. \( \displaystyle \frac{5}{2}\)
    24. Solution A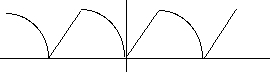
  24. The function \(f(x)\) below is called a sawtooth wave. Which of the following statements about this function is true?
    1. \( f(x)\) is continuous everywhere
    2. \( f(x)\) is differentiable everywhere
    3. \( f(x)\) is continuous everywhere but the values of x for which \(f(x) = 0\)
    4. \( f(x)\) is an even function
    5. \( f(x)\) is a one-to-one function.
    25. Solution A
  25. Find the derivative of \(y = x^2e^{x^2} \)
    1. \( 2xe^{x^2}(x^2 + 1)\)
    2. \( 2xe^{x^2}\)
    3. \( 2x^3e^{x^2}\)
    4. \( 4x^2e^{x^2}\)
    5. \( x^4e^{x^2}\)
    26. Solution A
  26. \( \displaystyle \int_{0}^{ \frac{\pi}{2}} e^{2 - \cos{x}} \sin{ x} \, dx = \)
    1. \( \displaystyle e^2 - e\)
    2. \( \displaystyle 1\)
    3. \( \displaystyle 0\)
    4. \( \displaystyle e^2\)
    5. does not exist
    27. Solution A
  27. The average value of \( \displaystyle f(x) = -\frac{1}{x^2}\) on \([\frac{1}{2}, 1]\) is
    1. -4
    2. -2
    3. \( \displaystyle -\frac{1}{2}\)
    4. 2
    5. undefined
    28. Solution B
  28. \( f(x) = \left| x^2 - 3x \right| \). Find \(f'(1)\)
    1. -3
    2. -1
    3. 1
    4. 3
    5. does not exist
    29. Solution C