BC Calculus: Midyear Review Worksheet 5

Questions have been taken from Lifshitz, Maxine, Calculus AB/BC Preparing for the Advanced Placement Examinations; Amsco, 2004

A graphing calculator is required for some questions.

  1. \(f(x) =\cos{x}\). Which of the following are true?
    1. \( \displaystyle \int_{-a}^{a} \cos{x} \, dx = 2\int_0^a \cos{x} \, dx \)
    2. \( \displaystyle \int_a^c \cos{x} \, dx + \int_c^b \cos{x} \, dx = \int_a^b \cos{x} \, dx \)
    3. \( \displaystyle \int_{-a}^{a} \cos{x} \, dx = 0\)
    1. I only
    2. II only
    3. I and II
    4. II and III
    5. I, II, and III
    2. Solution C
  2. \( \displaystyle \frac{d}{dt} \int_0^{2t} \frac{1 -\cos{x}}{x} \, dx =\)
    1. \( \displaystyle \frac{1 - cos 2t}{ t}\)
    2. \( \displaystyle \frac{1 - cos 2t}{2t}\)
    3. \(\sin {(2t)}\)
    4. \(2 \sin {(2t)}\)
    5. \( \displaystyle \frac{2t \sin {(2t)} + \cos {(2t)}}{2t^2}\)
    3. Solution A
  3. Find the slope of the tangent to the graph of \(x\ln {y} + e^x = y\) at the point (0, 1)
    1. -1
    2. 0
    3. 1
    4. 2
    5. undefined
    4. Solution C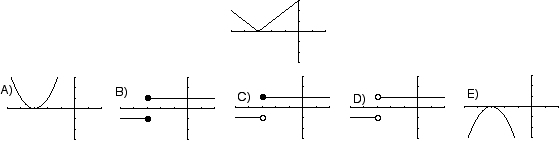
  4. The graph of \(y = f(x)\) is shown below. Which of the following could be the graph of \(y = f'(x)\)?
    5. Solution D
  5. Let \(f(x) = \sqrt{x^2 - x}\). Find \(f'(1)\)
    1. \( \displaystyle -\frac{1}{2}\)
    2. 0
    3. \( \displaystyle \frac{1}{2}\)
    4. 1
    5. does not exist
    6. Solution E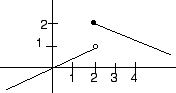
  6. Which of the following is NOT true about the function \(f(x)\) shown below?
    1. \(f(2) = 2\)
    2. \( \displaystyle \lim_{x \to 2^-} f(x) = 1\)
    3. \( \displaystyle \lim_{x \to 2} f(x) = 1 \)
    4. \( \displaystyle f'(0) = \frac{1}{2}\)
    5. \(f'(x)\) does not exist at \(x = 2 \)
    7. Solution C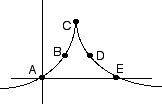
  7. In the figure below, at which point is \( \displaystyle \frac{dy}{dx}\) the smallest?
    8. Solution D
  8. \(f'(x) = 0.25(x+1)^3(2x + 5)(x - 3)^2\). The graph of \(f(x)\) has
    1. no critical points
    2. one relative minimum and one relative maximum
    3. two relative minima and one relative maximum
    4. two relative minima and two relative maxima
    5. three relative minima and one relative maximum
    9. Solution B
  9. Consider the function \( \displaystyle y = \frac{x}{x^2 + 1}\). At what value of \(x\) is \( \displaystyle \frac{dy}{dx}\) the largest?
    1. \(- \sqrt{3}\)
    2. -1
    3. 0
    4. 1
    5. \(\sqrt{3}\)
    10. Solution C
  10. The acceleration a in \( \displaystyle \frac{\text{ft}}{\text{sec}^2}\) of an object is given by the equation \(a = -v\), where \(v\) is the velocity of the object in \( \displaystyle \frac{\text{ft}}{\text{sec}}\). If the initial velocity is 1 \( \displaystyle \frac{\text{ft}}{\text{sec}}\), then the position function could be
    1. \(Ce^{-t} \)
    2. \(Ce^t \)
    3. \(e^t + C\)
    4. \(e^{-t} + C\)
    5. \(-e^{-t} + C \)
    11. Solution E
  11. For \(t \geq 0\), a particle moves along a line with position \(s(t) = 2t^3 - 9t + 1\). What is the acceleration when the particle is at rest?
    1. -9
    2. -6.348
    3. 0
    4. 1
    5. 14.697
    12. Solution E
  12. A taxi driver is going from LaGuardia Airport to Kennedy Airport at an average speed of \(v\) miles per hour. The distance is thirty miles and gas costs $1.33 per gallon. The taxi consumes gas at a rate of \( \displaystyle f(v) = 2 + \frac{v^2}{600}\) gallons per hour and \( 10 \leq v \leq 55\). What average speed will minimize the total cost of fuel?
    1. 10.0 mph
    2. 25.823 mph
    3. 54.46 mph
    4. 40.00 mph
    5. 34.641 mph
    13. Solution E